[PR]
2025年12月16日
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
卓球台を大きくするには
2017年01月07日
正月に、とんねるずのスポーツ王は俺だ!! 5時間スペシャルをやっていました。
特に卓球の試合を見ていて、気になったことがあったので今回はこれを考えます。
第三試合、「面積が2倍の卓球台」を使っていました。
しかし面積を2倍にするために出てきたオプションの台は幅が縦と横で同じ…
これで元の2倍の大きさの卓球台を作ったら、縦と横の大きさはどうなっているのでしょうか?
卓球台の大きさは幅1525mm、長さ2740mmだそうです。
縦・横同じ長さだけ延長して、元の2倍の面積を持つ卓球台を作りましょう。
大きくするための台の幅をxと置くとx > 0です。
次回は、この大きさの卓球台の縦横比について考えたいと思います。
特に卓球の試合を見ていて、気になったことがあったので今回はこれを考えます。
第三試合、「面積が2倍の卓球台」を使っていました。
しかし面積を2倍にするために出てきたオプションの台は幅が縦と横で同じ…
これで元の2倍の大きさの卓球台を作ったら、縦と横の大きさはどうなっているのでしょうか?
卓球台の大きさは幅1525mm、長さ2740mmだそうです。
縦・横同じ長さだけ延長して、元の2倍の面積を持つ卓球台を作りましょう。
大きくするための台の幅をxと置くとx > 0です。
(1525 + x) × (2740 + x) = 2 × 1525 × 2740
1525 × 2740 + (1525 + 2740)x + x2 = 2 × 1525 × 2740
(中略)
x ~ 821 ∵x > 0
次回は、この大きさの卓球台の縦横比について考えたいと思います。
PR
64 = 65問題の件
2017年01月05日
64 = 65の話をご存知でしょうか。
8 × 8の正方形を4つに切り取り、並べ替えるだけで面積が5 × 13になる問題です。
今回は、なぜ面積が変わるのかについて考えてみようと思います。
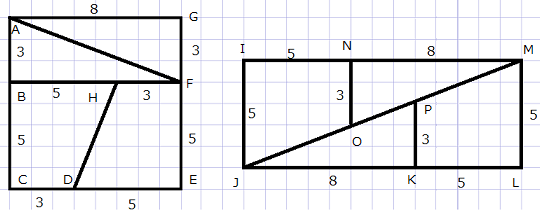
※説明のため各頂点に記号を振りました。
図の△ABF、△FGAが△PKJ、△ONMに移動し、台形も同様に移動したようだけに見えます。
しかし、全体の長方形として見ると、面積が1だけズレてしまうのです。
何故でしょうか。
左側の図の、対角線の傾き(の絶対値)は、横に13、縦に5です。
では、右側の図の、AFの傾き(の絶対値)はいくつでしょうか。
横に8、縦に3です。
この2つが同じ図形だとすると、その傾きも同じになるはずです。
傾きを整理してみましょう。
左の図の横:縦から考える。
13 : 5
= 13 × 8 / 13 : 5 × 8 / 13
= 8 : 40 / 13
~ 8 : 3.077
8 : 3ではなく8 : 3.077になりました。
この僅かな違いが、面積を1だけズラしていたのです。
定規を当てても納得できなかった方(私のことです)も、これなら納得できるでしょうか……?
8 × 8の正方形を4つに切り取り、並べ替えるだけで面積が5 × 13になる問題です。
今回は、なぜ面積が変わるのかについて考えてみようと思います。
※説明のため各頂点に記号を振りました。
図の△ABF、△FGAが△PKJ、△ONMに移動し、台形も同様に移動したようだけに見えます。
しかし、全体の長方形として見ると、面積が1だけズレてしまうのです。
何故でしょうか。
左側の図の、対角線の傾き(の絶対値)は、横に13、縦に5です。
では、右側の図の、AFの傾き(の絶対値)はいくつでしょうか。
横に8、縦に3です。
この2つが同じ図形だとすると、その傾きも同じになるはずです。
傾きを整理してみましょう。
左の図の横:縦から考える。
13 : 5
= 13 × 8 / 13 : 5 × 8 / 13
= 8 : 40 / 13
~ 8 : 3.077
8 : 3ではなく8 : 3.077になりました。
この僅かな違いが、面積を1だけズラしていたのです。
定規を当てても納得できなかった方(私のことです)も、これなら納得できるでしょうか……?
ポケモンのパーティー
2017年01月05日
ポケモンにおいてパーティーは何通りあるのか考えてほしいとリクエストをいただきました。
ありがとうございます。
先日ポケットモンスター サン・ムーンが発売されましたね。
2017/01/04時点で公開されているポケモン総数は801匹だそうです。
このポケモン、完全にランダムに選んでパーティーを組んだら、何通りのパーティーが考えられるのでしょうか。
まず、私の知識から条件を考えます。
さらに問題を簡単にするため、今回は次の条件を追加しようと思います。
先頭のポケモンは801通り考えられる。 ①
1. 2番目以降のポケモンが0匹のとき
2番目以降のパーティーは、全て空席の1通り。
すなわち、8020通り。
2. 2番目以降のポケモンが1匹のとき
2番目以降のパーティーは、801匹または卵の802通り。
すなわち、8021通り。
3. 2番目以降のポケモンが2匹のとき
2番目以降のパーティーは、8022通り。
4. 2番目以降のポケモンが3匹のとき
2番目以降のパーティーは、8023通り。
5. 2番目以降のポケモンが4匹のとき
2番目以降のパーティーは、8024通り。
6. 2番目以降のポケモンが5匹のとき
2番目以降のパーティーは、8025通り。
①及び1-6から、ポケモンのパーティー総数は以下のようになる。
801 * (8020 + 8021 + 8022 + 8023 + 8024 + 8025)
= 801 * Σ_(0≦n≦5) (1 * 802n)
= 801 * (8026 - 1) / (802 - 1)
= 266,100,818,073,753,663
26京6100兆8180億7375万3663通りと計算できました。
ポケモンの数も増えましたね。
ありがとうございます。
先日ポケットモンスター サン・ムーンが発売されましたね。
2017/01/04時点で公開されているポケモン総数は801匹だそうです。
このポケモン、完全にランダムに選んでパーティーを組んだら、何通りのパーティーが考えられるのでしょうか。
まず、私の知識から条件を考えます。
- ポケモンは801匹+卵の中から重複を許して選ぶ
- 最初の1匹以外のポケモンのエントリー順は考慮しない※バトル時に出る順とエントリー順は一致しないため。ポケルスとか何だかんだあった気はしますが忘れました
- エントリーするポケモンの数は1以上6以下、ただし卵だけでは認められない
さらに問題を簡単にするため、今回は次の条件を追加しようと思います。
- 先頭のポケモンは卵でない
先頭のポケモンは801通り考えられる。 ①
1. 2番目以降のポケモンが0匹のとき
2番目以降のパーティーは、全て空席の1通り。
すなわち、8020通り。
2. 2番目以降のポケモンが1匹のとき
2番目以降のパーティーは、801匹または卵の802通り。
すなわち、8021通り。
3. 2番目以降のポケモンが2匹のとき
2番目以降のパーティーは、8022通り。
4. 2番目以降のポケモンが3匹のとき
2番目以降のパーティーは、8023通り。
5. 2番目以降のポケモンが4匹のとき
2番目以降のパーティーは、8024通り。
6. 2番目以降のポケモンが5匹のとき
2番目以降のパーティーは、8025通り。
①及び1-6から、ポケモンのパーティー総数は以下のようになる。
801 * (8020 + 8021 + 8022 + 8023 + 8024 + 8025)
= 801 * Σ_(0≦n≦5) (1 * 802n)
= 801 * (8026 - 1) / (802 - 1)
= 266,100,818,073,753,663
26京6100兆8180億7375万3663通りと計算できました。
ポケモンの数も増えましたね。
数学における文法について
2017年01月04日
国語や英語に文法があるように、数学にも文法があります。
今回は私の中でルールにしている数学語を紹介します。
式の中で主語となる部分は先に書きます。
これはほとんどの言語で共通だと思います。
y = 3x
「yは3xに比例する」
「yはxの関数」ですので、主語はyです。
よって、yを先に書きます。
x > 4
「xは4より大きい」
xの範囲、値について言いたいとき、主語はxです。
よって、xを先に書きます。
n ∈ N
「nは自然数に属する」
nの条件を言いたいとき、主語はnです。
これも今まで通り、nを先に書きます。
不等式は小さい順に並べます。
これにより、不等式を見るだけで数直線をイメージできます。
0 < x < 1
xは0より大きく1より小さい
数直線のOと不等式の0を重ねて、不等式に対して平行に数直線を引く。と言われたら割と想像しやすくありませんか?
なお、これはあくまで数学上のルールで、数学以外の科学では柔軟に対応するのがよいと思います。
少なくとも高校生までが使う数式は日本語に読み替えることができます。
読み替えたとき、日本語として不自然がないように努力しています。
× よってxは、x=2
よってxは、xは2。
文章で吃る必要はありません。
○ よって、x=2
よって、xは2。
文章として締めたいなら
よって、x=2となる。
よって、xは2となる。
問題を解くとき、公式を使うと思います。
公式は変形せず正しく使って、先人への敬意や公式覚えてるアピールをします。
(sin x + cos x)(sin y + cos y)
=sin x sin y + sin x cos y + cos x sin y + cos x cos y
=(sin x cos y + cos x sin y) + (cos x cos y + sin x sin y) ←cos cosを先に書きます。
=sin (x + y) + cos (x - y)
思いついたら追記します。
今回は私の中でルールにしている数学語を紹介します。
① 主語は先に書く
式の中で主語となる部分は先に書きます。
これはほとんどの言語で共通だと思います。
関数
y = 3x
「yは3xに比例する」
「yはxの関数」ですので、主語はyです。
よって、yを先に書きます。
不等式・等式
x > 4
「xは4より大きい」
xの範囲、値について言いたいとき、主語はxです。
よって、xを先に書きます。
集合
n ∈ N
「nは自然数に属する」
nの条件を言いたいとき、主語はnです。
これも今まで通り、nを先に書きます。
② 不等式は小さい順
不等式は小さい順に並べます。
これにより、不等式を見るだけで数直線をイメージできます。
0 < x < 1
xは0より大きく1より小さい
数直線のOと不等式の0を重ねて、不等式に対して平行に数直線を引く。と言われたら割と想像しやすくありませんか?
なお、これはあくまで数学上のルールで、数学以外の科学では柔軟に対応するのがよいと思います。
③ 数式を日本語の文として読む
少なくとも高校生までが使う数式は日本語に読み替えることができます。
読み替えたとき、日本語として不自然がないように努力しています。
× よってxは、x=2
よってxは、xは2。
文章で吃る必要はありません。
○ よって、x=2
よって、xは2。
文章として締めたいなら
よって、x=2となる。
よって、xは2となる。
④ 公式を正しく引用する
問題を解くとき、公式を使うと思います。
公式は変形せず正しく使って、先人への敬意や公式覚えてるアピールをします。
(sin x + cos x)(sin y + cos y)
=sin x sin y + sin x cos y + cos x sin y + cos x cos y
=(sin x cos y + cos x sin y) + (cos x cos y + sin x sin y) ←cos cosを先に書きます。
=sin (x + y) + cos (x - y)
思いついたら追記します。
時計を見ながら比
2017年01月02日
比について教えて欲しいという要望があり、昨日から比について考えています。
時計を眺めていたら少し比について考えることがあったので、今日はその話をまとめます。
1時間は60分です。1分は60秒です。
これを、比っぽい表記で書いてみましょう。
1(時間) : 60(分) ①
1(分) : 60(秒) ②
ここで問題です。この2つの比をまとめることはできるでしょうか?
②を、第一回の記事を参考に、「:」の両側を60倍してみましょう。
60(分) : 3600(秒) ②'
これと①を見比べると…同じ60(分)が含まれています。
このように、たくさんの項目がある比はまとめて記述することができます。
1(時間) : 60(分) : 3600(秒)
時計を眺めていたら少し比について考えることがあったので、今日はその話をまとめます。
1時間は60分です。1分は60秒です。
これを、比っぽい表記で書いてみましょう。
1(時間) : 60(分) ①
1(分) : 60(秒) ②
ここで問題です。この2つの比をまとめることはできるでしょうか?
②を、第一回の記事を参考に、「:」の両側を60倍してみましょう。
60(分) : 3600(秒) ②'
これと①を見比べると…同じ60(分)が含まれています。
| 1(時間) | 60(分) | |
| 60(分) | 3600(秒) |
1(時間) : 60(分) : 3600(秒)
