[PR]
2025年06月14日
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
面積2倍って……
2017年01月09日
前回、前々回の記事で、卓球台の面積を2倍にするためには幅をどれだけ大きくすればいいか考えてきました。
ここで思った人がいるでしょう。
「面積2倍って、卓球台2つ並べればよくね?」
今回はこの件について考えてみようと思います。
卓球台を2つ並べてひとつの卓球台とすれば、確かに面積は2倍になります。
では、面積が2倍になったとき、縦・横の比はどうなるのでしょうか。
卓球台の面積は、何度も確認しているように1525 × 2740(mm)です。
では、2つの卓球台を横に並べて使うことを考えてみましょう。
1525mmの幅のみが2倍され、これが長さになりますから、縦横比は
2740 : 1525 × 2 = 2740 : 3050
となります。
ちなみに、このように面積を2倍にしても縦横比が変わらない図形は、ノート、プリントなどに使われており、その縦横比は白銀比と呼ばれています。
ここで思った人がいるでしょう。
「面積2倍って、卓球台2つ並べればよくね?」
今回はこの件について考えてみようと思います。
卓球台を2つ並べてひとつの卓球台とすれば、確かに面積は2倍になります。
では、面積が2倍になったとき、縦・横の比はどうなるのでしょうか。
卓球台の面積は、何度も確認しているように1525 × 2740(mm)です。
では、2つの卓球台を横に並べて使うことを考えてみましょう。
1525mmの幅のみが2倍され、これが長さになりますから、縦横比は
2740 : 1525 × 2 = 2740 : 3050
となります。
ちなみに、このように面積を2倍にしても縦横比が変わらない図形は、ノート、プリントなどに使われており、その縦横比は白銀比と呼ばれています。
PR
卓球台の縦横比に関して(続き)
2017年01月07日
前回、卓球台の面積を2倍にするためには卓球台の4辺をすべて821mm伸ばせばよいことをまとめました。
今回は、卓球台の面積を2倍にしつつ、卓球台の形を変えない方法について考えていきたいと思います。
卓球台の面積を倍にしたのはいいが、卓球台らしからぬ形になっては面倒ですね。
形を変えずに大きさを変えるための考え方として、相似があります。
相似とは、2つの図形のうち一方を拡大・縮小すれば他方と重なる状態をいいます。
一方をr倍したとき、その図形は縦も横もr倍になっているため、面積はr2倍になるのです。
では、面積を2倍にしようと思ったら、1辺は何倍にすればよいのでしょうか。
√2倍です。
つまり、1525 × 2740(mm)の卓球台をその形を変えずに大きくするには、
幅 : 1525 × √2 = 2157 (mm)
長さ : 2740 × √2 = 3875 (mm)
にすればよいことになります。
今回は、卓球台の面積を2倍にしつつ、卓球台の形を変えない方法について考えていきたいと思います。
卓球台の面積を倍にしたのはいいが、卓球台らしからぬ形になっては面倒ですね。
形を変えずに大きさを変えるための考え方として、相似があります。
相似とは、2つの図形のうち一方を拡大・縮小すれば他方と重なる状態をいいます。
一方をr倍したとき、その図形は縦も横もr倍になっているため、面積はr2倍になるのです。
では、面積を2倍にしようと思ったら、1辺は何倍にすればよいのでしょうか。
√2倍です。
つまり、1525 × 2740(mm)の卓球台をその形を変えずに大きくするには、
幅 : 1525 × √2 = 2157 (mm)
長さ : 2740 × √2 = 3875 (mm)
にすればよいことになります。
卓球台を大きくするには
2017年01月07日
正月に、とんねるずのスポーツ王は俺だ!! 5時間スペシャルをやっていました。
特に卓球の試合を見ていて、気になったことがあったので今回はこれを考えます。
第三試合、「面積が2倍の卓球台」を使っていました。
しかし面積を2倍にするために出てきたオプションの台は幅が縦と横で同じ…
これで元の2倍の大きさの卓球台を作ったら、縦と横の大きさはどうなっているのでしょうか?
卓球台の大きさは幅1525mm、長さ2740mmだそうです。
縦・横同じ長さだけ延長して、元の2倍の面積を持つ卓球台を作りましょう。
大きくするための台の幅をxと置くとx > 0です。
次回は、この大きさの卓球台の縦横比について考えたいと思います。
特に卓球の試合を見ていて、気になったことがあったので今回はこれを考えます。
第三試合、「面積が2倍の卓球台」を使っていました。
しかし面積を2倍にするために出てきたオプションの台は幅が縦と横で同じ…
これで元の2倍の大きさの卓球台を作ったら、縦と横の大きさはどうなっているのでしょうか?
卓球台の大きさは幅1525mm、長さ2740mmだそうです。
縦・横同じ長さだけ延長して、元の2倍の面積を持つ卓球台を作りましょう。
大きくするための台の幅をxと置くとx > 0です。
(1525 + x) × (2740 + x) = 2 × 1525 × 2740
1525 × 2740 + (1525 + 2740)x + x2 = 2 × 1525 × 2740
(中略)
x ~ 821 ∵x > 0
次回は、この大きさの卓球台の縦横比について考えたいと思います。
64 = 65問題の件
2017年01月05日
64 = 65の話をご存知でしょうか。
8 × 8の正方形を4つに切り取り、並べ替えるだけで面積が5 × 13になる問題です。
今回は、なぜ面積が変わるのかについて考えてみようと思います。
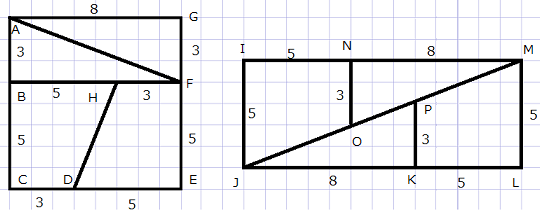
※説明のため各頂点に記号を振りました。
図の△ABF、△FGAが△PKJ、△ONMに移動し、台形も同様に移動したようだけに見えます。
しかし、全体の長方形として見ると、面積が1だけズレてしまうのです。
何故でしょうか。
左側の図の、対角線の傾き(の絶対値)は、横に13、縦に5です。
では、右側の図の、AFの傾き(の絶対値)はいくつでしょうか。
横に8、縦に3です。
この2つが同じ図形だとすると、その傾きも同じになるはずです。
傾きを整理してみましょう。
左の図の横:縦から考える。
13 : 5
= 13 × 8 / 13 : 5 × 8 / 13
= 8 : 40 / 13
~ 8 : 3.077
8 : 3ではなく8 : 3.077になりました。
この僅かな違いが、面積を1だけズラしていたのです。
定規を当てても納得できなかった方(私のことです)も、これなら納得できるでしょうか……?
8 × 8の正方形を4つに切り取り、並べ替えるだけで面積が5 × 13になる問題です。
今回は、なぜ面積が変わるのかについて考えてみようと思います。
※説明のため各頂点に記号を振りました。
図の△ABF、△FGAが△PKJ、△ONMに移動し、台形も同様に移動したようだけに見えます。
しかし、全体の長方形として見ると、面積が1だけズレてしまうのです。
何故でしょうか。
左側の図の、対角線の傾き(の絶対値)は、横に13、縦に5です。
では、右側の図の、AFの傾き(の絶対値)はいくつでしょうか。
横に8、縦に3です。
この2つが同じ図形だとすると、その傾きも同じになるはずです。
傾きを整理してみましょう。
左の図の横:縦から考える。
13 : 5
= 13 × 8 / 13 : 5 × 8 / 13
= 8 : 40 / 13
~ 8 : 3.077
8 : 3ではなく8 : 3.077になりました。
この僅かな違いが、面積を1だけズラしていたのです。
定規を当てても納得できなかった方(私のことです)も、これなら納得できるでしょうか……?
| HOME |
